Serge's World

For anyone who has studied calculus, the Newton-Rhapson method should be familiar. To those who have not, I do apologize if I lose you, but will try to make it easy.

The Newton-Rhapson method is a way to find the roots of a function using approximations.

So, for the non-maths people out there, a function is denoted by f(x) and can be any equation, for example f(x) = x^2 + 3, or f(x) = sin(x). Now, the roots of a function are defined by f(x) = 0, so it is wherever the function equals zero.

Another important concept here is the derivative f’(x). This is the rate of change of the function f(x), but by going any deeper, I know I will lose the non-maths guys, and I am sure any of you who know some maths already know about derivatives.

The Newton-Rhapson method tries to find the values of the root by approximating the root, and then iterating using the procedure a’ = a - f(a)/f’(a) where a is the approximated root, and a’ is the closer approximation. The procedure is then repeated replacing a with the new a’ value, as many times as is needed to achieve the required accuracy.

So how the function that generates the fractal works, first we take our canvas, and iterating through each pixel in the canvas, we get x and y values, which are made up of the minimum values - which are passed as a parameter, so that we can view any part of the Cartesian space - and then add to that the column (or row) we are on multiplied by the scaling factor.

Now that we have our values we are going to pass into our function, and have set up a few values before we iterate, we start the iteration.

We keep on iterating, using the Newton-Rhapson method to find new values for x and y, and finally finished iteration when either we have reached a point where the values are as accurate as they are ever going to be, or else we have reached the amount of iterations we are going to allow.

Now that we have done that, we can select the color to draw at that particular point. We have created an array of 16 colours, and then depending on values of x and y, we use certain colours, based on the iteration in which we reached our value.

If x is larger than 0, then the first 5 colours are used. If y > 0 and x is less than -0.3 then the next 5 colours are used, and for everything else the last 6 colours are used.
Read More »

Julia sets are very similar to Mandelbrot sets, and if you have not yet looked at my post on generating Mandelbrot sets, then I suggest you take a look. Most of the background is the same.

The only major difference is between Julia sets and the Mandelbrot set is that the Mandelbrot iteration is based on the equation Z = Z^(Power 1) + Z^(Power 2) + C, where C is the point Z(0). The Julia set is based on the equation Z^(Power 1) - Z^(Power 2) - L, where L is a constant complex number.

We iterate through each point, using the centre of the screen as the origin (0,0). For each point then, we iterate up to our maximum depth, using the Julia formula now instead of the Mandelbrot one, and break when the absolute value of Z reaches 2.

We can then draw the point, using the same method as we used for drawing the Mandelbrot point.
Read More »

Of all the fractals around, the Mandelbrot set is one of the most famous, largely because it creates quite a complex and beautiful image. In my view anyway.

The actual method of calculating a Mandelbrot is relatively easy to follow. easy, that is, if you know what complex numbers are. A complex number is an imaginary number that is based on the squareroot of -1, which does not exist as a real number, and is usually denoted by i. A complex number is made up of a real part and an imaginary part, in the form Z = x_i_ + y, where x and y are both real numbers, except that x is multiplied by the imaginary i.

Right, so enough maths before I lose you all completely.

So for our function that generates the Mandelbrot, we pass it various parameters which control the scaling, size and offset, which can be used to zoom in on particular areas. This is unimportant in the actual calculation of the fractal, except as modifiers for the calculations so that they calculate the correct area. The important parameters are the iterations, and the powers, as they will directly influence the calculations.

The Complex class which is used in the code to define the complex numbers in a complex number class which I have written, which I wont go into detail here, but is included with the full source code. The workings of the complex number class is covered in a separate post

So, on to how to calculate the Mandelbrot. we first set the two complex numbers, Z and C to the origin (0, 0).

Now we iterate from the top left to bottom right corners of our screen, using the centre of the screen as the coordinates (0,0). When we draw the points physically, we will add the offset to draw on the right location, since (0,0) is the top left corner in most images, but for the calculations , the top left corner will be (-width / 2, -height / 2).

So for each iteration, we adjust the real and imaginary portions of Z using the scaling and offset values, and then set C to Z.

Now, we iterate up to the iteration depth we specified. Each time we iterate, we apply the formula Z = Z^(Power 1) + Z^(Power 2) + C. For a normal Mandelbrot, these values are set to 2 and 0, so for the standard Mandelbrot, this equation becomes Z = Z^2 + C. You are encouraged to experiment with other values to get some really interesting looking images.

If the absolute value of Z is greater than 2, we then stop iterating, and take note of which iteration number we stopped at. This will be used to determine what colour we are going to plot at that point.

So, now we are ready to plot our point, and using the DrawComplexPoint function we plot the point. At this point, we add the offsets needed, as mentioned above, to move our coordinate system to the correct places for our image.

What this function also does is selects the colour to draw. In our code, there are 16 predefined colours in an array, which is selected based on the modulus of the iteration number we found in the previous step.
Read More »

A T-Square fractal is a relatively simple affair.

The procedure to create a T-Square starts off with a square canvas on which we are going to draw. It will work with rectangular canvases as well, but then the results will look slightly different.

When we call the GenerateTSquare function, we need to pass to it the coordinates of the first square, which, to get the best fit into our canvas, we calculate the lengths of the sides of the square to be half the canvas sides, and then centre the square, essentially making the top left corner a quarter of the way to the right and down of the origin.

The first thing we do is draw a solid square using our coordinates.

Now, until we reach our desired recursion depth, we generate four new squares, which have half the width and height, and make the centres of each of these squares to be centred on each of the four corners of the original square.

This process is then repeated until we have recursed far enough.

public void GenerateTSquare(Graphics g, int iIterations, double iLeft, double iTop, double iWidth, double iHeight, Color oColor)
{
	g.FillRectangle(new SolidBrush(oColor), (float)iLeft, (float)iTop, (float)iWidth, (float)iHeight);
	if (iIterations > 1)
	{
		double dNewWidth = iWidth / 2.0;
		double dNewHeight = iHeight / 2.0;

		GenerateTSquare(g, iIterations - 1, iLeft - (dNewWidth / 2.0), iTop - (dNewHeight / 2.0), dNewWidth, dNewHeight, oColor);
		GenerateTSquare(g, iIterations - 1, iLeft + iWidth - (dNewWidth / 2.0), iTop - (dNewHeight / 2.0), dNewWidth, dNewHeight, oColor);
		GenerateTSquare(g, iIterations - 1, iLeft - (dNewWidth / 2.0), iTop + iHeight - (dNewHeight / 2.0), dNewWidth, dNewHeight, oColor);
		GenerateTSquare(g, iIterations - 1, iLeft + iWidth - (dNewWidth / 2.0), iTop + iHeight - (dNewHeight / 2.0), dNewWidth, dNewHeight, oColor);
		

	}
}

The full source code is available at https://github.com/sjmeunier/fractalize.

Originally posted on my old blog, Smoky Cogs, on 30 Sep 2009

Brownian motion is described by an essentially random motion, which, one of the most famous examples is the movement of a speck of dust floating on the surface of a glass of water.

For our fractal, the random element of the brownian motion, while essentially still being random is constrained by the end points. To create the fractal, we start with an array of 128 double values. This array could in theory be any size, and is not a fixed requirement.

Now, the first element and last element are our starting and ending points of our path. In the code, these points are randomly generated, but could just as easily be set explicitly.

Before we look at the Generate function, I am going to look at the Gauss function. This function takes three parameters - the seed for the random number generator (so we can create the same fractal by passing the same seed), Mu and Sigma.

The Mu value is the base displacement we want the path to move, and the Sigma value is a multiplier for the random element.

A random number is generated, which is then multiplied by Sigma, which is then added to Mu to give us the displacement of the value for that step in the calculation.

private double Gauss(int iSeed, double fMu, double fSigma)
{
	double fx;
	int i;

	fx = 0;
	for (i = 0; i < 12; i++)
	{
		fx = fx + (new System.Random(iSeed).NextDouble());
	}
	fx = fx - 6.0;
	return fMu + fSigma * fx;
}

Fern fractals are another class of iterative fractals, a type of iterative function system, that draws rather good images of ferns. And with a bit of tweaking of the input variables, the ferns of various sizes and shapes can be created using the same code.

To create a fractal fern you first need to supply a rather large amount of input variables that will control the shape of the fern. So in the application, the variables are stored in a few arrays.
Read More »

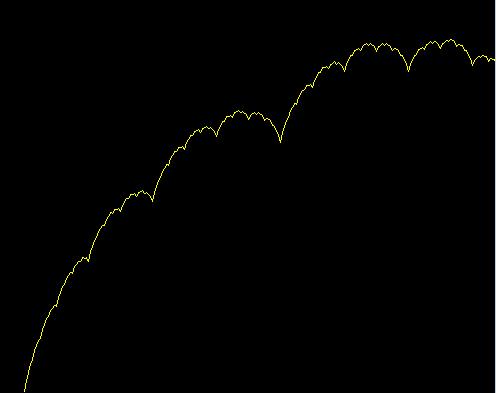
Sierpinski triangles and squares are relatively easy fractals to draw, and although the principle is the same I will handle the two separately.

For Sierpinski triangles, you take your initial triangle (an equilateral triangle works nicely) and then finding the midpoints of each side and connecting them, break up the triangle into four new triangles. Then for each of the three triangles on the outside, repeat this process until you reach the desired recursion depth. The middle triangle is left alone, and remains unfilled. When you reach the recursion depth you require, you can then colour the triangle the desired colour.

Sierpinksi squares work in a similar way, except, instead of using the midpoint, you divide each edge into three pieces, and then split up the initial square into nine new squares. Repeat this process for the eight outer squares, leaving the middle square, as in for the triangles, alone. Once you reach the desired recursion depth, you then colour the square the desired colour.

So, then, the code to generate this is as follows. There is nothing tricky at all about it. In both cases, if the recursion depth is not yet met, the points are calculated, and the function is called recursively for each new shape, and if you have recursed far enough, then draw the shape based on the desired colour and coordinates. The coordinates of the initial shapes are passed as doubles to the functions, such as x1, y1 etc.
Read More »

Plasma fractals generate images based on random varying of vlaues across the image, allowing for vairations which include plasma, terrain or cloud-like images.

So, what is a plasma fractal exactly? A plasma fractal is generated by taking a rectangle with a width x and height y. Then to each corner in the rectangle, assign a random value between 0 and 1.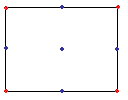

The next step is to find the midpoint of each side, and at that point, calculate the average value of the two points that this point is bisecting. A midpoint is also calculated, which is in the centre of the rectangle, which is the average of all four corners plus a random displacement.

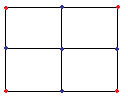Then for each of the four rectangle bounded by the new points, repeat the process, until all the pixels have been calculated.

After the values have been calculated, the values can be converted to colours using any method you like. Using the raw values unaltered will create a greyscale image very well with only adjusting the value to put it in the correct range.

Now, in the code to do this, first, we have a few global variables

public double gRoughness;
public double gBigSize;
FastRandom rnd;

The roughness is amount in which we are going to vary the value by for the midpoint.gBigSize is defined as the width plus the height of the image we are generating. FastRandom is a random number generator, which works exactly like the builtin random number generator, except that it is faster.

Our starting point is the Generate function that return a two-dimensional array of values where each entry in the array corresponds to an xy coordinate and the value is the calculated value, which will be converted into a colour.
Read More »

Here is something that was a very pleasant surprise when I saw it. There actually exists a programming language, the Shakespeare Programming Language, written by Karl Hasselström and Jon Åslund, which is unlike anything I have seen before.

Instead of conventional programming logic, the source code for the Shakespeare Programming Language looks more like a Shakespearean play than any code you have seen before.

Firstly, “actors” in the play take the role of conventional variables, and must be listed at the beginning.

The program is split up into acts and scenes, and these “actors” can then enter and exit the scene, much as they would in a play.

The dialog spoken by each character in the scene determines the actual programming logic.

To fully give you an understanding of how this all works, here is the source code from the the Shakespeare Programming Language site for their Hello World program.

The Infamous Hello World Program.

Romeo, a young man with a remarkable patience.
Juliet, a likewise young woman of remarkable grace.
Ophelia, a remarkable woman much in dispute with Hamlet.
Hamlet, the flatterer of Andersen Insulting A/S.


                    Act I: Hamlet's insults and flattery.

                    Scene I: The insulting of Romeo.

[Enter Hamlet and Romeo]

Hamlet:
 You lying stupid fatherless big smelly half-witted coward!
 You are as stupid as the difference between a handsome rich brave
 hero and thyself! Speak your mind!

 You are as brave as the sum of your fat little stuffed misused dusty
 old rotten codpiece and a beautiful fair warm peaceful sunny summer's
 day. You are as healthy as the difference between the sum of the
 sweetest reddest rose and my father and yourself! Speak your mind!

 You are as cowardly as the sum of yourself and the difference
 between a big mighty proud kingdom and a horse. Speak your mind.

 Speak your mind!

[Exit Romeo]

                    Scene II: The praising of Juliet.

[Enter Juliet]

Hamlet:
 Thou art as sweet as the sum of the sum of Romeo and his horse and his
 black cat! Speak thy mind!

[Exit Juliet]

                    Scene III: The praising of Ophelia.

[Enter Ophelia]

Hamlet:
 Thou art as lovely as the product of a large rural town and my amazing
 bottomless embroidered purse. Speak thy mind!

 Thou art as loving as the product of the bluest clearest sweetest sky
 and the sum of a squirrel and a white horse. Thou art as beautiful as
 the difference between Juliet and thyself. Speak thy mind!

[Exeunt Ophelia and Hamlet]


                    Act II: Behind Hamlet's back.

                    Scene I: Romeo and Juliet's conversation.

[Enter Romeo and Juliet]

Romeo:
 Speak your mind. You are as worried as the sum of yourself and the
 difference between my small smooth hamster and my nose. Speak your
 mind!

Juliet:
 Speak YOUR mind! You are as bad as Hamlet! You are as small as the
 difference between the square of the difference between my little pony
 and your big hairy hound and the cube of your sorry little
 codpiece. Speak your mind!

[Exit Romeo]

                    Scene II: Juliet and Ophelia's conversation.

[Enter Ophelia]

Juliet:
 Thou art as good as the quotient between Romeo and the sum of a small
 furry animal and a leech. Speak your mind!

Ophelia:
 Thou art as disgusting as the quotient between Romeo and twice the
 difference between a mistletoe and an oozing infected blister! Speak
 your mind!

[Exeunt]

To find a more indepth explanation of how it works, go take a look at the Shakespeare Programming Language site.

Originally posted on my old blog, Smoky Cogs, on 27 Oct 2010

I recently blogged about Whitespace, being a language that was written primarily to be as obscure as possible. Well, Intercal is one of the old-timers in this category. It was conceived all the way back in 1972.

What I enjoyed about this language is that I don’t think there is a single sentence on their website, nor in their manual, which is not making some sort of joke. these are a bunch of guys who don’t take themselves seriously at all. For example, according to the manual, the full name of the compiler is “Compiler Language With No Pronounceable Acronym”, which is, for obvious reasons, abbreviated “INTERCAL”.

I have got to say that the code for something written in Intercal is not quite as incomprehensible as some other languages, but it certainly has got a completely different sense to any other language you may find. To give an example, to end program execution, the code is PLEASE GIVE UP. That should be some indication of the language. Not to mention, that it can output numbers natively in roman numerals.

Go on, I know you want to go and check it out…just heed the warning on the main page – Abandon All Sanity, Ye Who enter Here.

Originally posted on my old blog, Smoky Cogs, on 29 Sep 2009